En matemáticas, las funciones de Mathieu son soluciones de la ecuación diferencial de Mathieu. Su comportamiento es bastante peculiar debido a los fenómenos que describe, como la resonancia paramétrica (situación en la que ciertas funciones pueden aumentar su amplitud considerablemente cuando reciben una fuerza o vibración a una frecuencia específica) y la existencia de sub-armónicos (las funciones de Mathieu pueden tener múltiples componentes de frecuencia submúltiplos de la frecuencia principal).
Estos fenómenos hacen que las funciones de Mathieu sean objetos de estudio interesantes en la teoría matemática.
Émile Mathieu descubrió estas funciones en 1865 mientras investigaba las vibraciones de una membrana elíptica. Durante sus estudios, se encontró con una serie de ecuaciones diferenciales que describen el comportamiento de la membrana en términos de funciones matemáticas específicas. Para entenderlo, imagina que tienes una cuerda vibrante o una membrana elástica que se mueve en ciertos patrones. La ecuación diferencial de Mathieu describe cómo estas vibraciones, como variable de la ecuación, se comportan en términos matemáticos, y las soluciones a la ecuación diferencial de Mathieu se llaman funciones de Mathieu.
Relacionado con estas funciones, existe el operador casi de Mathieu. Un operador es una función o asignación que nos da una regla para modificar objetos matemáticos de alguna manera.
Este operador es conocido como operador casi de Mathieu porque es una aproximación del operador completo (la ecuación anterior) utilizado en las funciones de Mathieu, y se obtiene al convertir dicha ecuación en una forma más conveniente para el análisis.
En lugar de trabajar con una ecuación diferencial, se utiliza una matriz que representa las propiedades de la ecuación.
El operador casi de Mathieu es una versión simplificada del operador de Mathieu original. Esta simplificación se realiza mediante la introducción de ciertas aproximaciones o restricciones en la ecuación diferencial original.
Esta matriz se puede diagonalizar, lo que significa que se puede convertir en una matriz cuyos elementos son cero excepto aquellos en la diagonal, siendo los números de la diagonal los valores propios de la matriz. Estos valores propios están relacionados con las propiedades de las funciones de Mathieu, como su frecuencia y forma.
El operador casi de Mathieu se deriva de la ecuación de Schrödinger, que es una ecuación fundamental en la mecánica cuántica, que describe una función de onda a lo largo del tiempo.
A principios de los años ochenta hubo mucho trabajo en la teoría matemática de los operadores de Schrödinger, y ahí apareció el famoso problema de los diez martinis. El nombre fue acuñado por Barry Simon en su artículo de 1982, página 487, titulado «El problema de los diez martinis: El operador casi de Mathieu tiene un espectro de Cantor», y apareció en una famosa lista de problemas sobre operadores de Schrödinger, y permaneció no resuelto hasta el año 2005. El nombre proviene del hecho de que Mark Kac ofreció en una reunión de la Sociedad Matemática Americana en 1981 diez martinis a cualquiera que lo resolviera.
Este operador tiene la siguiente fórmula:
H^(λ,α)ωu(n) = u(n+1)+u(n-1)+2λcos(2π(ω+nα))u(n)
y se aplica sobre una función u(n) junto con los valores λ, α, ω obteniendo una secuencia de valores que depende del índice n.
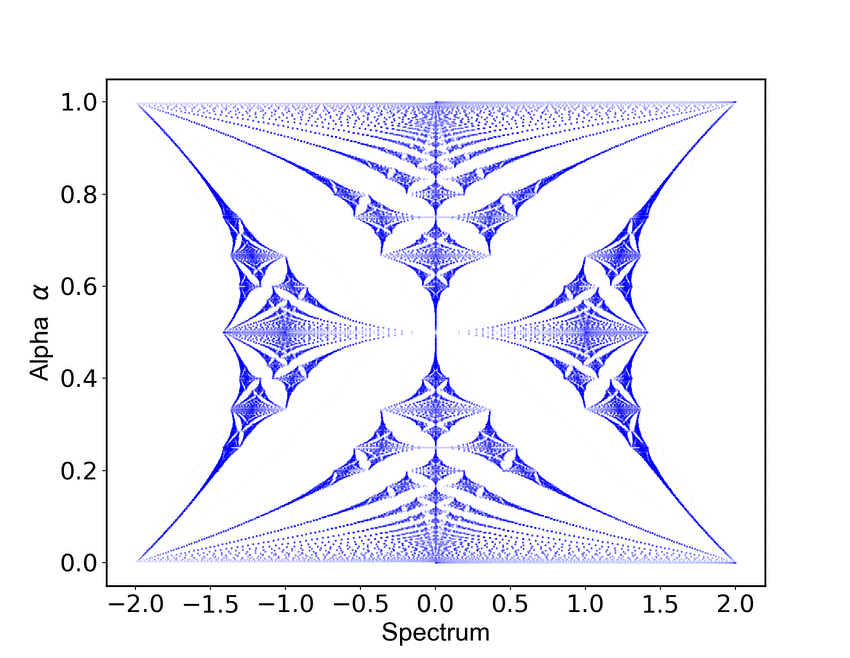
La característica destacada del operador casi de Mathieu es que su espectro (el conjunto de valores propios de la secuencia) es un conjunto de Cantor para todos los valores irracionales de α, y λ mayores que cero.
Para encontrar los valores propios correspondientes a la expresión, se puede considerar el problema de encontrar las soluciones no triviales de la ecuación λu(n) = u(n+1) + u(n-1) + 2λcos(2π(ω+nα))u(n). Una forma de abordar esto es considerar la ecuación en forma matricial. Si consideramos un número finito de términos en la secuencia (por ejemplo, si tomamos n en un rango finito), podemos representar la ecuación como un sistema de ecuaciones. Luego, los valores propios se pueden encontrar al resolver el polinomio característico (una ecuación cuyas soluciones, o raíces, son los valores propios) de la matriz.
El problema era ver que el conjunto de valores propios o autovalores asociados a la ecuación, tiene la estructura de un conjunto de Cantor.
El concepto del conjunto de Cantor se relaciona con el espectro del operador casi de Mathieu debido a la forma en que se distribuyen los valores propios en dicho espectro, presentando una estructura fractal característica, ya que, un conjunto de Cantor es aquel cuyo cardinal es 2^ℵ0 (es tan grande el conjunto como los números reales, es decir, bastante grande), y que tiene forma de fractal.
Todo esto fue demostrado por Avila y Jitomirskaya al resolver el famoso «problema de los diez martinis» en 2005 (también uno de los problemas de Barry Simon), después de varios resultados anteriores (incluyendo genéricamente y casi con certeza con respecto a los parámetros).
Resultados parciales previos incluyen a Bellissard y Simon en 1982, quienes demostraron la estructura de Cantor para pares de cierta forma de (b, ω).
Sinai demostró en 1987 que si ω satisface una condición Diofantina (o diofántica), entonces el espectro del operador es un conjunto de Cantor siempre que |b| (valor absoluto de b) sea suficientemente pequeño (qué tan pequeño depende de la condición Diofantina precisa).
En cuanto a los números irracionales no Diofantinos, los llamados números de Liouville, Choi, Elliot y Yui (1991) demostraron el Problema de los Diez Martinis para una clase de estos números de Liouville. Un número de Liouville es un número real «x» tal que, para cualquier entero positivo «n», existen otros dos enteros «p» y «q», con «q» > 1, que satisfacen que 0 < |x – p/q| < 1/q^n, es decir, que son casi racionales.
Joaquim Puig, en el artículo «Espectro de Cantor para el operador de casi Mathieu», y como parte de su tesis doctoral, demostró que si |b| ≠ 2, y ω es diofántico, es decir, que ω es un número irracional que no puede ser muy bien aproximado por números racionales (matemáticamente, se dice que ω es diofántico si existen constantes c y α tales que para todo número racional p/q (donde p y q son enteros positivos y q ≠ 0) se cumple que |ω – p/q| ≥ c/q^α), entonces el espectro del operador de Mathieu casi es un conjunto de Cantor. La idea de la prueba consiste en combinar herramientas provenientes de la teoría espectral y los sistemas dinámicos.
Por la resolución de este problema, Svetlana fue galardonada en el Congreso Internacional de Matemáticos de 2022 con el Premio Olga Ladyzhenskaya de matemática-física.